Wind power is generated by using wind turbines to harness the kinetic energy of wind. Wind blowing across the rotors of a wind turbine causes them to spin. The spinning of rotors converts a portion of the kinetic energy of the wind into mechanical energy. A generator further converts this mechanical energy into electricity.
Wind power can be generated at utility scale, offshore location and at distributed or small scale. Utility scale wind power uses turbines larger than 100 kilowatts to deliver power to the grid. Offshore wind power, as the name implies, is generated by installing large turbines at offshore locations. Distributed wind power is produced from turbines of 100 kilowatts or less and supply power directly to a home or building or for running any machine.
Turbine outputs depend on volume of air (quantity), velocity of air and mass or density of air. Not all the kinetic energy of wind incident on a turbine can be converted into power. Efficiency of extraction of wind power from kinetic energy by a turbine is determined by Betz’s law. A conventional wind turbine cannot be more than 59% efficient as per this law, i.e. it can at the most convert 59% of kinetic energy into power or electricity. Utility scale wind turbines can achieve their peak output at 75-80% of this limit.
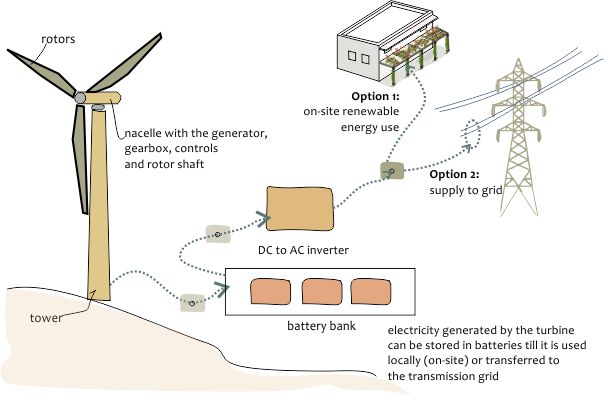
Wind energy generation system
In a wind turbine, the rotors are connected to a shaft which transfers the spinning motion to the coil of a generator. In between, a gearbox is also installed to increase the spinning speed of the shaft. Electricity generated by the generator is either fed into the grid or transferred to a battery bank for storage. Inverters are provided to convert the DC current to AC.
The most important component of a wind energy generation system is the turbine itself. Parts described below are common to turbines but the assembly method may vary.
- Tower –Usually a steel or concrete tubular structure that vary in height from 200 to 300 feet. Smaller wind turbines, less than 10 kilowatts, use poles instead of free standing towers. Horizontal turbines require towers.
- Rotors blades and rotor hub
- Nacelle or drive train – Houses the gearbox, rotor shaft, generator (or alternator) and controls
- Gearbox – This synchronizes the motion of the rotor and the generator, and is generally used for speeding of the generator. Gearboxes are not needed for smaller turbines.
- Generator – These convert the mechanical energy of the rotors into electricity. Both synchronous/ permanent magnet generators and asynchronous or induction generators can be used. The former can be used without a gearbox and are also more efficient. Asynchronous generators are more durable and need less maintenance, and can be synchronised with the grid more easily. Alternators are also used instead of generators.
- Electronics and controls – Essentially wind assessment instruments that guide the rotation and pitch of the rotors for maximum power output. Diagnostic equipment, and other controls for cooling the generator may also be included.
- Tail vane or yaw is used for aligning horizontal wind turbines with wind.
- Braking
- Pitch controls for managing the pitch of the rotors
Wind turbines with direct drive systems do not require a gearbox. The rotor hub is directly connected to the generator by a fixed axle or shaft. Maintenance costs for such turbines are lower as there are fewer moving parts and no gear oil to be changed.
Cost breakup of a wind turbine
The turbine itself is the costliest component of a wind energy generation system, ranging from 75-80% of the total, rest being for installation and preparing the site. Rotor blades and the tower are the more expensive than the rest of the components of a wind turbine put together.
Wind turbine size
Utility scale wind turbines can vary in size from 50 kW to 750 kW. They are mounted at heights between 200 to 300 feet and the rotors can be more than 100 feet in length. Turbines used in residences, commercial buildings or for specific purposes like water pumps are usually less than 50 kW in size. Rotors of these turbines are about 10 to 30 feet in diameter, and are mounted at a height of 30 feet or more.
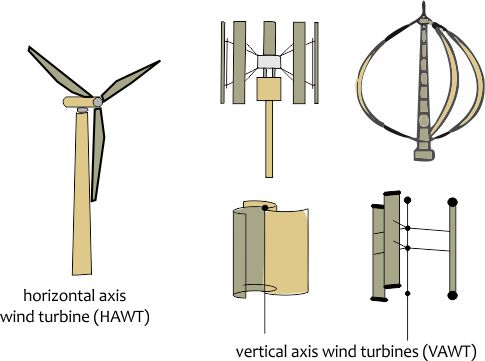
Types of wind turbines
Turbines extract energy from wind based of either of the two aerodynamic forces: drag and lift. Machines working on the principle of lift are inherently more efficient as the forces are applied in the direction of wind flow while in drag driven machines, forces are applied in the reverse direction.
Horizontal axis wind turbines (HAWT) continually face in the direction of wind and are lift driven machines. Rotors in a HAWT can be in front of the tower on which it is supported and facing the wind (windward), or behind it and away from the wind (leeward). Rotors or blades in most horizontal axis turbines are placed upwind to the tower. Horizontal wind turbines are equipped with sensors which determine both the direction and velocity of the wind. Number of rotors may vary but 2-3 rotors are the most efficient configuration and most easily available.
Vertical axis wind turbines (VAWT) are not dependant on the wind direction and are more suitable for area of highly variable wind direction. Shaft containing the gearbox, generator etc. is vertical. Consequently they are more suitable for distributed generation in buildings. Generator and gearbox is installed on the ground for vertical turbines which renders them easier for maintenance. Darrieus or egg beater is a lift force driven vertical axis turbine and Savonius is a drag driven type of vertical axis turbine. Savonius wind turbines are the most widely used drag type turbines because of their robustness.
Horizontal wind turbines are preferred over vertical turbines, especially in commercial operations. Utility scale turbines are mostly horizontal turbines. Vertical turbines have low rotational speed, high torque and lower power coefficient, and resultantly less efficient than horizontal wind turbines. They are also more difficult to design as the modelling of air flow around a vertical turbine is not easy.
Smaller wind turbines are designed to work at lower speeds.